Humanoid Robot Control with PyPnC

Whole Body Control and DCM Planner based Locomotion in PyBullet

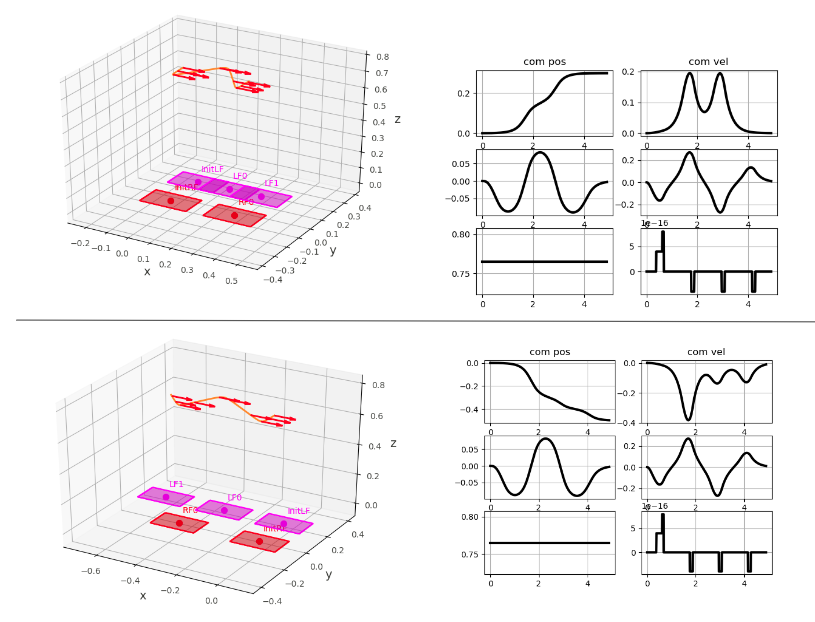
This project aims to simulate a humanoid robot’s walking and balancing using Whole Body Control (WBC) and Divergent Component of Motion (DCM) planner using URDF models of Boston Dynamics’ ATLAS in the PyBullet environment. This project was implemented from PyPnC as a part of The University of Texas at Austin’s Design and Control of Human-Centered Robotics (ASE389) course.

Humanoid Modeling under Multi-Contact Constraints

Challenges in humanoid robots involve high dimensionality, underactuation, and operation under geometrical and multi-contact constraints. A humanoid robot’s behavior is determined by not only the displacements of its articulated joints but also interactions of its bodies in contact.

*Figure 1: Kinematic representation of a humanoid robot The free moving base is represented as a virtual spherical joint in series with three prismatic virtual joints. Reaction forces appear at the contact points due to gravity forces pushing the body against the ground. Contact constraints are expressed as rigid constraints with zero velocities and accelerations at the supporting bodies [1].*

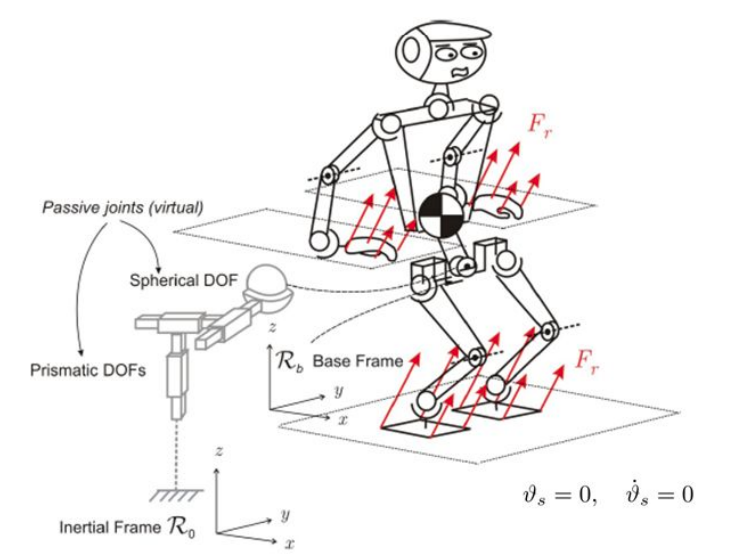
The equation of motion (EOM) which is subjected to actuation torques and external forces can be derived using the Euler-Lagrange equation.

Equation of Motion 1

Equation of Motion 2

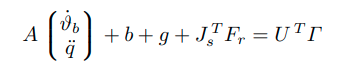
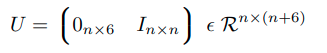
where A is the (n + 6) × (n + 6) inertia matrix, b and g are (n + 6) × 1 vectors of Coriolis/centrifugal and gravity forces. For more detail, refer to Compliant Control of Whole-Body Multi-Contact Behaviors in Humanoid Robots

Joint Space Control, Operational Space Control, and Whole Body Control

*Figure 2: A 3-link planar robot arm*

EOM above can be developed into different control schemes, and they can be shown with a simple 3-link planar robot arm which is more intuitive than a complex humanoid robot to explore features of each control scheme.

*Figure 3: Joint Space Control with PD Controller*

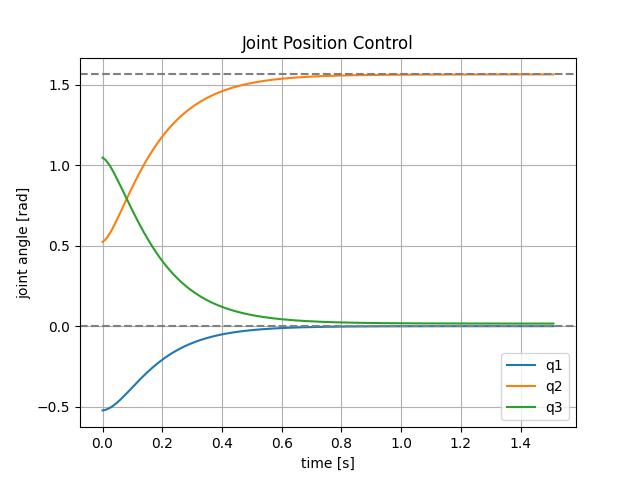
Firstly, joint space control takes desired joint configuration as an input and outputs joint torques with feedback control.

*Figure 4: Operational Space Control with PD Controller*

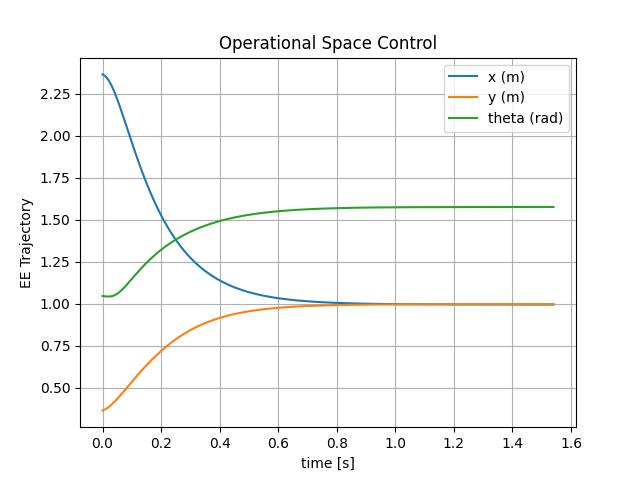
Secondly, operational space control takes control the end-effector’s motion in the task space by controlling the forces and torques in the control space. Operational space control is a more high-level and task-specific control as it enables the specification of desired end-effector behaviors in the task space, rather than specifying joint angles or velocities in the control space.

*Figure 5: Prioritized Whole Body Control (Task and Posture Control)*

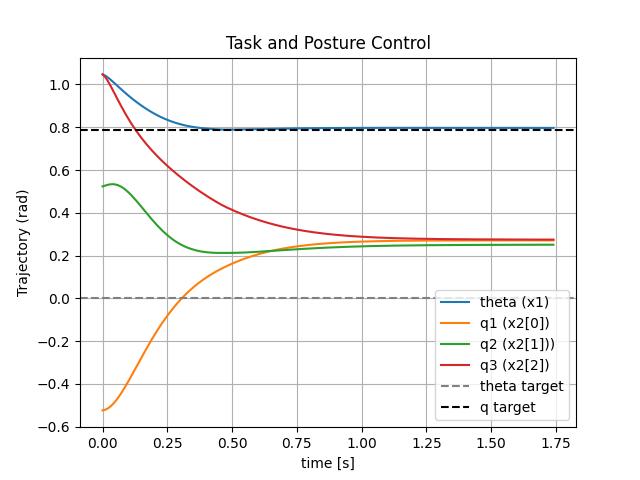
Finally, prioritized whole body control can perform two tasks which conflict with each other. Figure 5 shows the desired joint configuration as [0,0,0] (task: x2) which configures the robot to stretch in a straight line while attempting to achieve the desired end-effector orientation as π/4 (task: x1) which is not feasible with the desired joint configuration at [0,0,0]. Prioritized whole body control law can set a higher priority of task x1 over task x2. In this case, the robot achieves the desired end-effector orientation while trying to minimize the error in the desired joint configuration. This control law ensures accomplishment of critical tasks over sub-tasks, and it enables whole-body compliant behaviors and exploits the redundancy of humanoids under geometric and contact constraints.

Whole Body Control: Stand and Balance

WBC for humanoid balancing can be formulated with an optimization problem which minimizes the joint acceleration and reaction forces. It can be represented as:

*Optimization Problem for WBC*

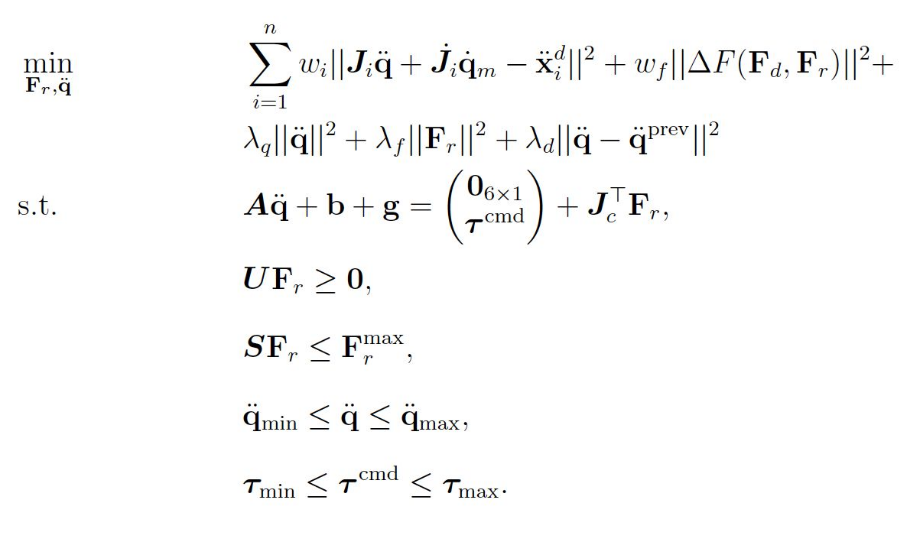
The optimization is subjected to the cost function, equality constraints, and inequality constraints, and boundaries of joint acceleration and command torques. The optimization problem is solved with a quadratic programming (QP) solver.

*Quadratic Programming Step 1*

*Quadratic Programming Step 2*

*Quadratic Programming Step 3*

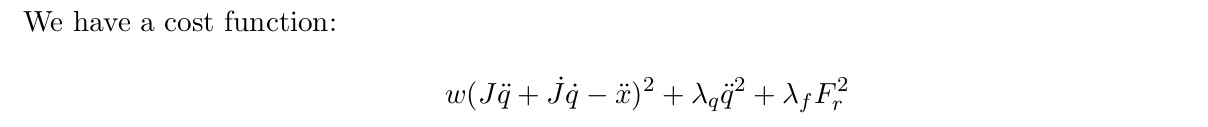
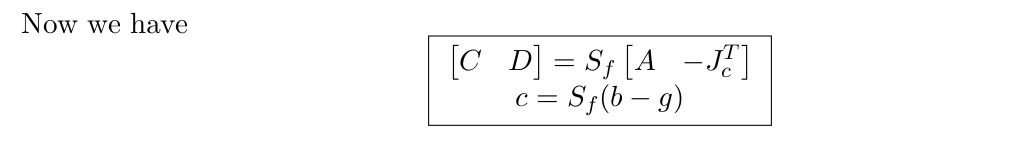
The cost function is a quadratic function of joint acceleration and reaction forces. The equality constraints are the EOM and the kinematic constraints which allow the robot to stand on the ground by the law of physics. The inequality constraints include the wrench term while the inequality vector is determined by the gravity and Coriolis term. The wrench term ensures that the direction of the normal force under gravity and Coriolis force prevent the foot from slipping and flipping. While Coulomb friction law defines the relationship between the frictional and normal force of two surfaces in contact, inequality constraints enforce a minimum normal force during the optimization. The inequality constraints also prevent saturation of the joint acceleration and command torques.

*Figure 6: Humanoid balancing with WBC*

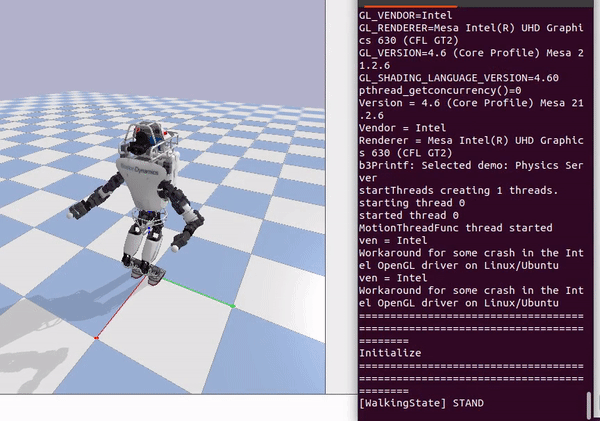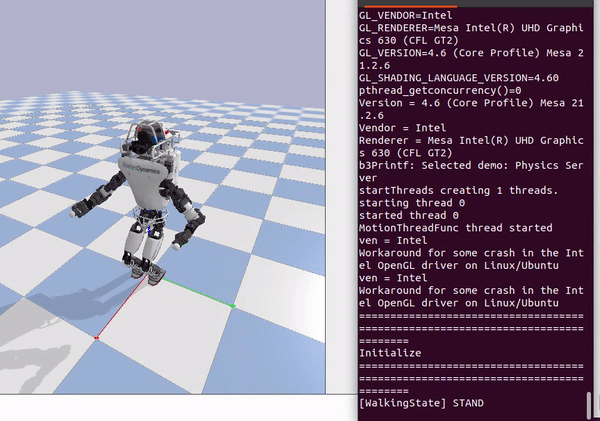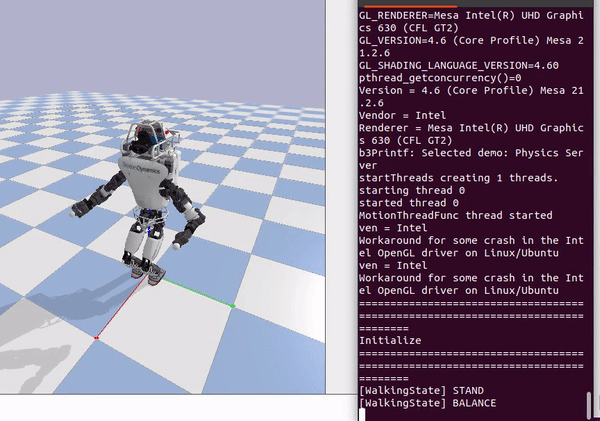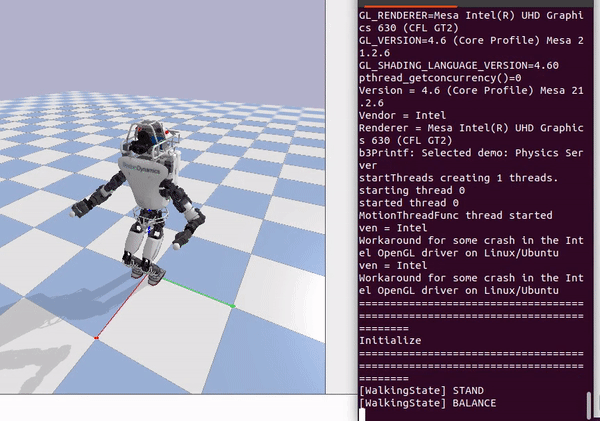
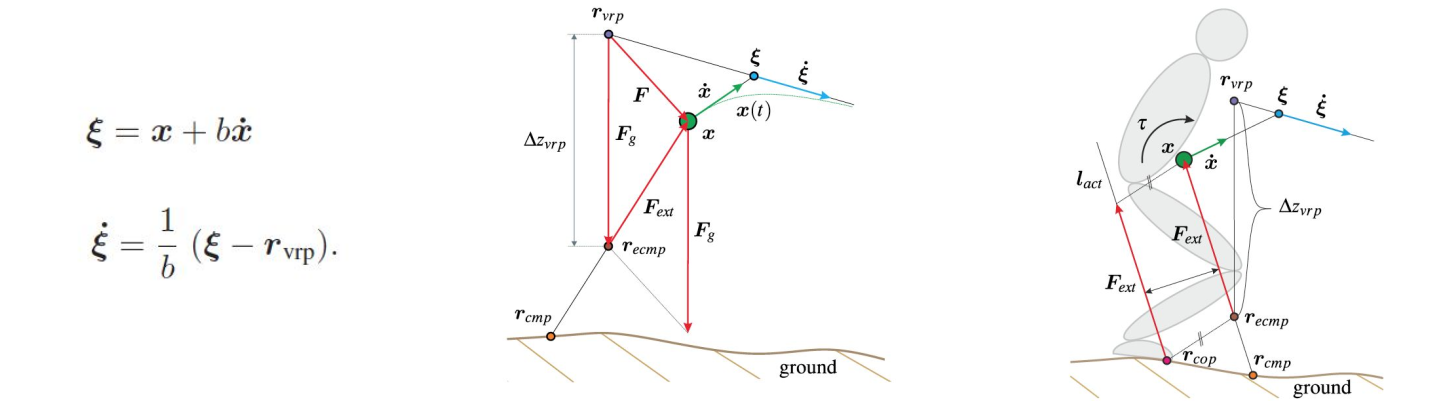
DCM Planner: Trajectory Generation

While DCM is a quantity in Cartesian space that is related to the COM position and velocity, DCM Planner generates walking patterns using the virtual repellent point (VRP) which is a point in Cartesian space that encodes both direction and magnitude of the external forces acting on the robot.

*Figure 7: DCM and VRP: COM tends to converge to DCM while VRP repels DCM*

*DCM Planner Step 1*

*DCM Planner Step 2*

*Figure 8: Forward Walking Trajectory (Top) and Backward Walking Trajectory (Bottom)*

Forward, Backward, and Sideway Walking

Click to watch the video