Impact Modeling with Euler-Lagrangian and Hamiltonian Mechanics

4 point mass system impact simulation in Python with SymPy

Results

*Jack Simulation GIF*

*Simulation Results Plot*

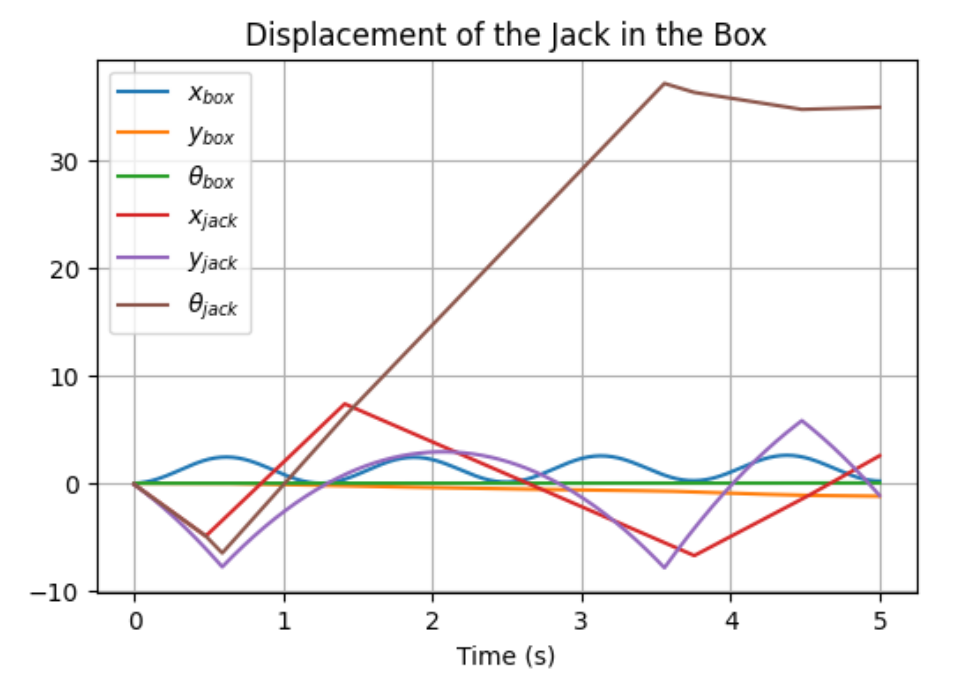
Simulation Setup

Transformation

*Transformation Diagram*

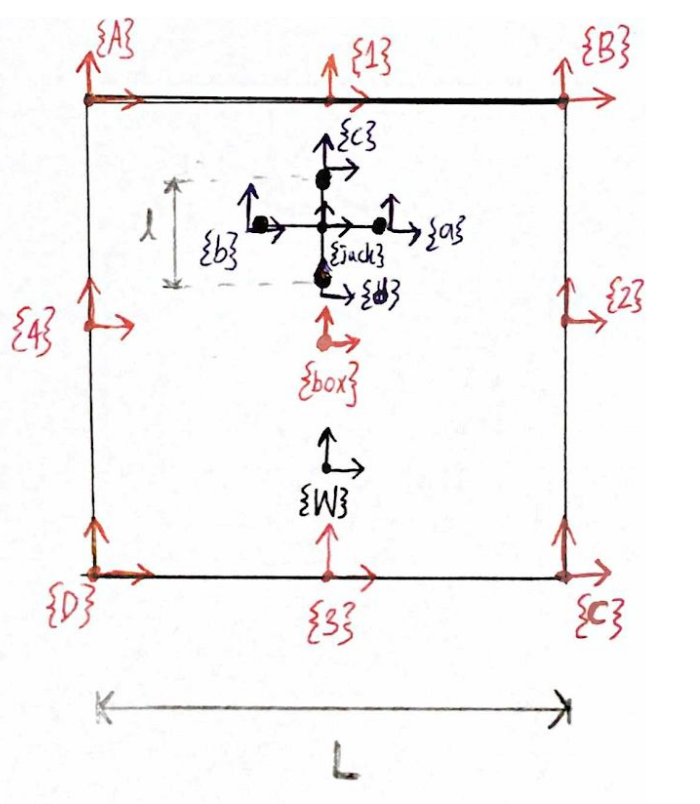
Vertexes of the bot were represented as {A}, {B}, {C}, and {D} while the edges of it were done as {1}, {2}, {3}, and {4}. Four point masses of jack were shown as {a}, {b}, {c}, and {d} while the World frame is shown as {W}.

Configuration

*Configuration Setup*

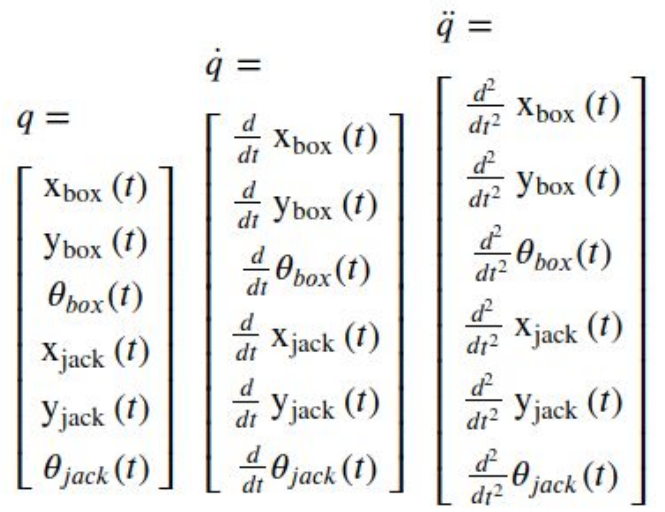
Both the box and jack are free to translate and rotate in an xy-plane.

LAGRANGIAN

*Velocity Components v1 and v2*

*Velocity Diagram*

*Potential Energy (PE)*

*Kinetic Energy (KE)*

*Lagrangian (L)*

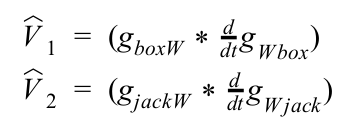
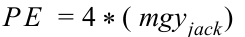
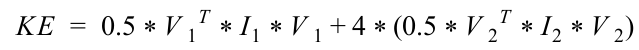
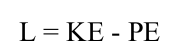
External Force

*External Force (F)*

*External Force Extended (Fext)*

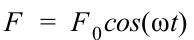
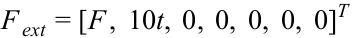
External force was applied assuming someone is shaking the box.

To ensure that jack hit all four edges of the box, the external force was applied in the x-direction since gravitational force will take the y-direction to make sure jack hits all four edges of the box.

Constraint

*Constraint List (qlist)*

*Constraint Formulation (qfor)*

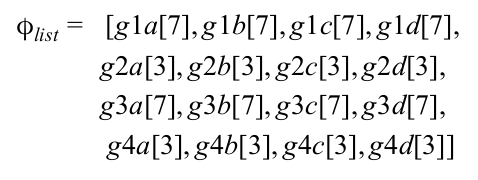
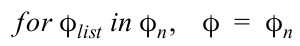
The jack has the constraint that it has to stay within the boundaries of the box.

Phi defines when the point masses of the jack make contact with the boundaries of the box, which are {1}, {2}, {3}, and {4}. There are multiple phi called phi_list in this system, and they are called in a for-loop so that it eliminates the necessity of making multiple impact update functions.

Phi can be expressed with the g matrix, while g_ij [3] represents the x-component and g_ij [7] the y-component.

Euler-Lagrangian

*Euler-Lagrangian Equation*

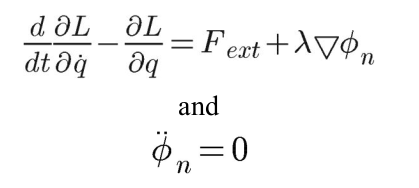
Impact Update Law

*Impact Update Equation (QPM)*

*Hamiltonian (HAM)*

*Impact Equations (EQ)*

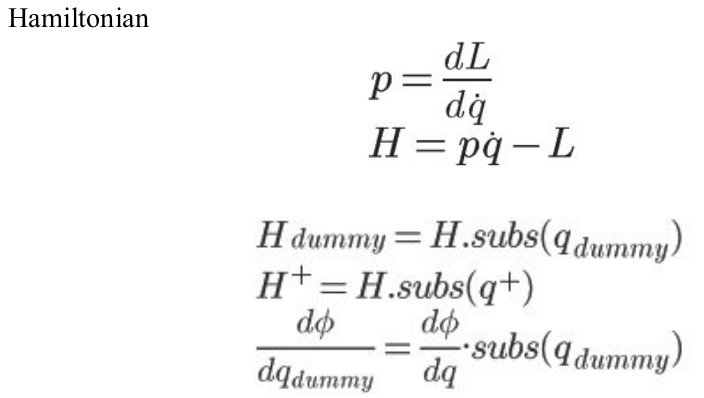
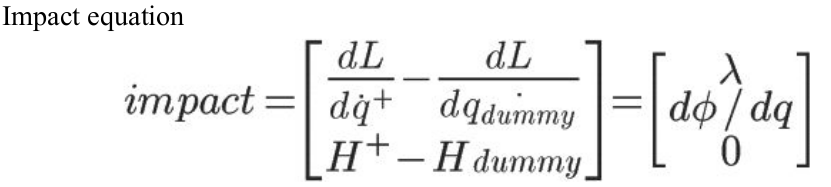
Function impact_condition takes phi_list and initial conditions, which include initial positions and velocities, lambdifies phi values, and tolerance to decide the impact condition.

Function impact_update takes initial conditions and impact equations to numerically update impacts.